Фазовые траектории и портреты режимов цепей
Фрагмент статьи по идентификации высших гармоник в электротехнических установках с использованием исследования несинусоидальных режимов по фазовым траекториям.
При анализе установившихся режимов электрических цепей несинусоидального тока существуют известные сложности, обусловливающие применение различных приближенных методов расчета. Для реактивных элементов оказывается невозможным применение символического метода расчета, даже при условии их линейности. А при учете нелинейности характеристик индуктивных катушек или конденсаторов даже приближенный аналитический расчет становится невозможным. Для решения указанных задач люди придумали достаточно эффективные численные методы, которые удаётся применить к задачам, сформулированным в гибридном, цепно-полевом формате. Для облегчения анализа получаемых результатов выполнен переход в автоматизированные расчетно-моделирующие системы. Однако результаты визуализации процессов зачастую отстают от уровня сложности решаемых задач.
Ниже показаны иллюстрации нестандартного подхода к анализу цепей с высшими гармониками. Подход несколько отличается от общей методологии ОТЦ и основан на построении математических моделей реактивностей в пространстве состояний, когда даже для стационарного режима цепи решается динамическая задача, с представлением всех реактивностей дискретными резистивными моделями. Задача решается на ЭВМ при помощи авторского софта, а сами модели прописываются автоматизированным способом в ASCII-коде. В результате решения получают характерный срез гармоник токов и напряжений любого элемента, позволяющий, оперируя массивами численных данных построить наборы фазовых характеристик всех реактивностей. Ниже на рисунках показана кучка фазовых портретов обыкновенного конденсатора в осях самой переменной состояния и её первой производной. И верхний и нижний ряды картинок являются производными от обыкновенной окружности стационарного режима линейной ёмкости на синусоидальном токе. На картинках указана циклическая частота несущей и полученный при этом результирующий набор гармоник реактивности.
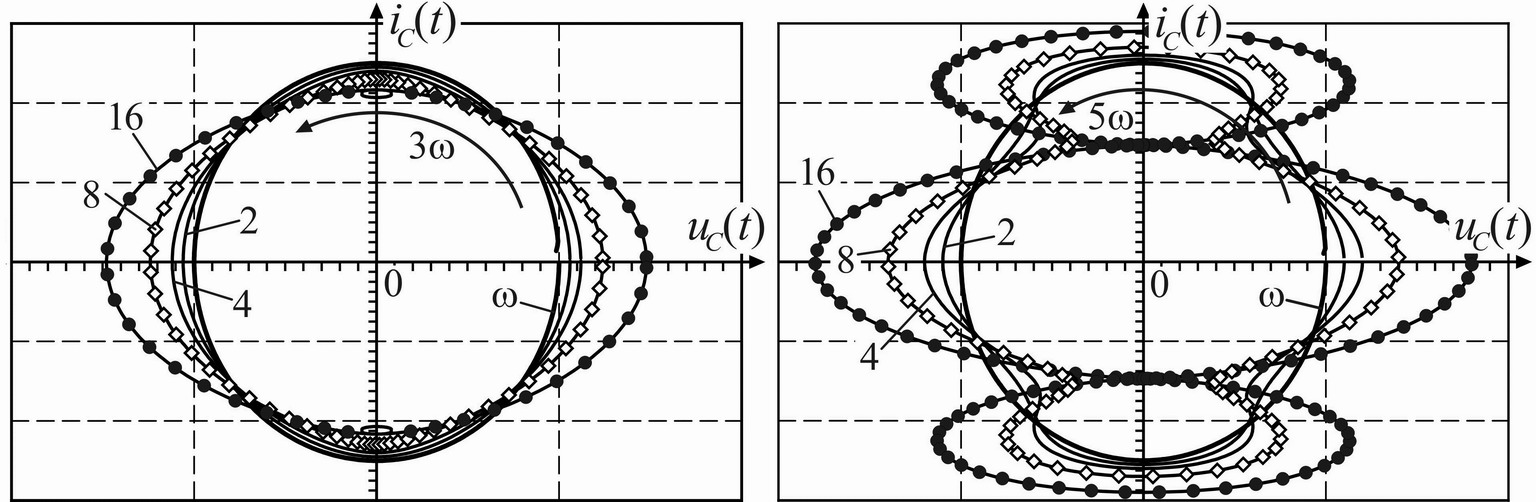
Представляется любопытным применить указанный подход к исследованию стационарных режимов цепей по фазовым кривым. Результатом исследования может стать выработка критериев качественной оценки режима цепи по характерным признакам для разного набора гармоник токов и напряжений.
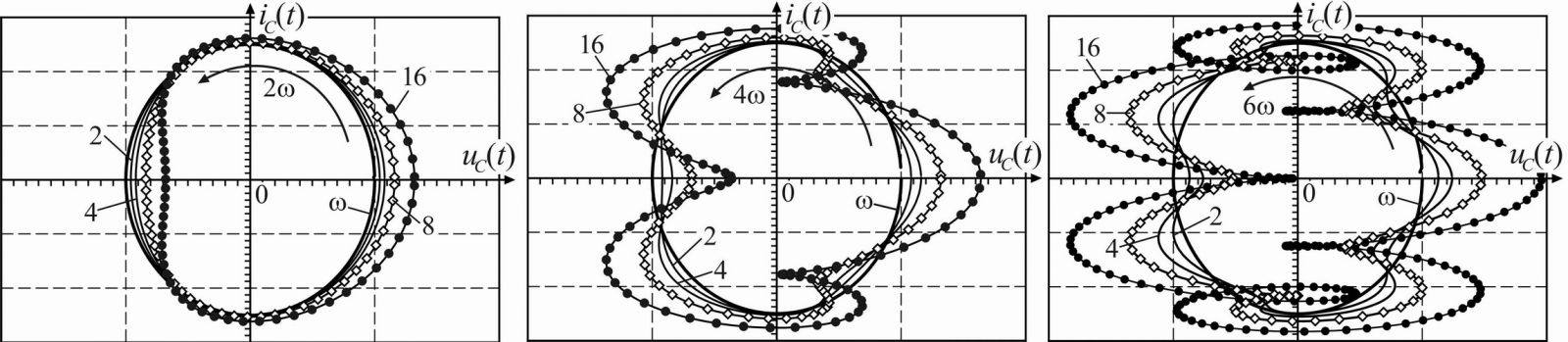
Как видно по рисункам, особенности симметрии характеристик можно использовать для идентификации вида искажений по типичному виду фазовых кривых, однозначно связанному с особенностями набора гармоник в установке. Любопытно, что нечётные гармоники дают осевую симметрию к обоим осям, а чётные симметричны только относительно оси аргумента. Соотношение амплитуд высших гармоник выбрано фиксированным, для повторяемости. К слову сказать, при построении моделей использован подход, основанный на оценке интенсивности переменных состояния емкостного элемента. Поэтому для индуктивностей получаются столь же характерные картинки, но с точностью до наоборот.
Дополнительные возможности диагностики и идентификации режима реактивностей предоставляет непосредственный доступ к численным данным анализа и возможность построения и манипуляций с трехмерными картинками высших гармоник в том же фазовом пространстве. Это значительно повышает эффективность визуализации процессов с использованием такого программного продукта, как Harvard Chart. Остальные известные продукты уступают Гарварду в этой части, даже не смотря на их определенные достоинства в области применения элементов анимации. Очень жаль, что указанный программный продукт не получил поддержки 32 и 64-разрядных операционных систем и не обновляется в настоящее время.
Евгений Бортник, Красноярск, Россия, февраль 2016