Цепно-полевой метод анализа электрических машин

Одним из подходов к анализу схем замещения электрических машин является разработка и применение цепно-полевого метода, основанного на уравнениях теории четырёхполюсников. Ниже рассмотрен фрагмент статьи, посвященной построению соответствующих цепных звеньев, учитывающих параметры режима электродвигателя, в виде взаимосвязанных векторов напряженности электрического и магнитного поля. Обобщенное е-н звено зубцово-пазовой зоны статора с произвольной формой паза. Выражения параметров единичного Е-Н звена, аппроксимирующего зубцово-пазовую зону статора с прямоугольным пазом были получены в литературе 1. Активный четырехполюсник содержит источник, аналогичный источнику тока, и параметры zi

где: wi – число витков, hi – высота паза, вi – ширина  паза, Zi – число зубцов.

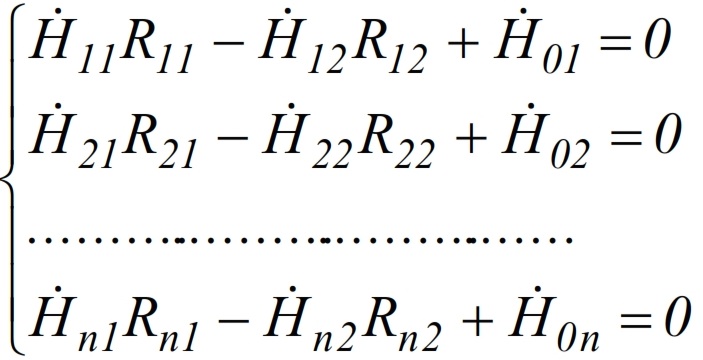
Очевидно, что Е-Н-схема замещения всей зубцово-пазовой зоны статора с произвольной формой паза будет представлять каскадное соединение активных четырехполюсников, аппроксимирующих элементарные слои, число которых (n), определяется заданной точностью расчета.

Найдем параметры активного четырехполюсника (рис. 3), аппроксимирующего всю зубцово-пазовую зону статора. Из условий эквивалентных преобразований для схемы, показанной на цепной схеме выше, на основании первого закона Кирхгофа имеем следующую систему уравнений:

Складывая уравнения системы, найдем распределение H, причем для цепной схемы, представленной на рисунке, на основании первого закона Кирхгофа имеем записанные выражения. Решая совместно уравнения (4-5), находят напряженность магнитного поля

где wэ – эффективное число витков фазы, Ri1, Ri2 – внутренний и внешний радиусы соответственно i-го слоя статора. Из условия равенства мощности источников в схемах на рисунках и равенства входных сопротивлений относительно первичных зажимов:

На основании второго закона Кирхгофа для схем, показанных на рисунках выше имеем:

Решая совместно уравнения (9, 10) с учетом выражения (8), получим:

Записав и решив совместно систему уравнений, полученную на основании законов Кирхгофа, найдем параметр:

Полученные выражения записаны для паза статора произвольной формы, следовательно, они представляют собой обобщенные параметры активного Е-Н-четырехполюсника, аппроксимирующего зубцово-пазовую зону статора. Результаты исследований, рассмотренные в статье, могут быть использованы для построения интегральной схемы замещения асинхронного двигателя специальной конструкции и анализа его выходных характеристик.

                  Евгений Бортник, Красноярск, Россия, 2012